1 Wenn die Arbeit zweieinhalb Mal so lang´ dauert  ODER das 2,5fache an Zeit beansprucht – Umwandlung von Brüchen in die Dezimalschreibweise

2 Mit Brüche muss man rechnen…mit Kommas aber auch – Addition und Subtraktion von Dezimalzahlen

3 Rechnen bei 10 oder 35 Grad: wir bleiben cool – Kreis und Winkel

4 Wenn aus dem Drittel einer Hälfte ein Sechstel wird – Multiplikation und Division von einfachen Brüchen und Dezimalzahlen

5 Plus plus minus mal: Rechnen in allen Variationen – Ganze Zahlen

6 Ein Bild sagt oft mehr als 1000 Worte – Daten erfassen, darstellen und interpretieren

Prozente und Zinsen – Vergleiche werden einfacher

Schnäppchenkäufer aufgepasst – Sonderangebote unter die Lupe genommen.

Relative Häufigkeiten und Wahrscheinlichkeiten

Wie muss unsere Klasse ein Glücksrad für das Schulfest konstruieren, damit bei einer fairen Gewinnchance ein Plus für die Klassenkasse übrigbleibt?

Porportionale, antiproportionale und lineare Zuordnungen

Einkäufe im Supermarkt, Auto- und Bahnfahrten, das Teilen einer Pizza mit Freunden – wir untersuchen Gesetzmäßigkeiten bei Zuordnungen.

Terme und Gleichungen

„Knack die Box“ – wie man mit Hölzchen und leeren Boxen Gleichungen legen und systematisch lösen kann und aus Streichholzmustern Terme entwickeln kann, durch die man sich aufwändiges Abzählen sparen kann.

Systeme linearer Gleichungen

Eine Gruppe mit 36 Jugendlichen besucht eine Eisdiele, in der es nur Tische für vier und sechs Personen gibt. Wie viele 4er und 6er Tische können sie komplett belegen – wir stellen lineare Gleichungen mit zwei Variablen auf und lösen diese mit Hilfe unterschiedlicher Verfahren.

Dreiecke

„Bis heute aktuell – Was schon Griechen in der Antike entdeckten“ – wie Beziehungen in Dreiecken und Halbkreisen bei der Bestimmungen von Längen, Höhen und Entfernungen helfen können.

Einführung in die Wahrscheinlichkeitsrechnung – Baumdiagramm

Eine Losbude macht Werbung  „Jedes 10. Los ein Hauptgewinn“. Gewinne ich dann auf jeden Fall, wenn ich 10 Lose kaufe?

Lineare Gleichungssysteme

3 Minuten nachdem Till zur Schule gefahren ist, fällt seiner Mutter auf, dass er sein Sportzeug vergessen hat. Schafft Sie es noch ihn einzuholen, wenn sie doppelt so schnell fährt?

Beispiel für Themenübergreifende Alltagsbeispiele – Anwenden von Wurzeln und Kreisberechnung

Der Turm soll eine quadratische Grundfläche von ca. 130 m² haben, welche Breite sollte das zu bebauende Grundstück dann mindestens haben?

Brauche ich ein kleineres Grundstück, wenn der Turm rund wird?

Einführung: Quadratische Funktionen

Lili möchte sich ein doppelt so großes Stück Pizza abschneiden wie Alex. Soll sie dann einfach beide Seitenlängen doppelt so lang machen?

• Tricks mit x, auch im Quadrat – quadratische Funktionen und quadratische Gleichungen
• Vom Mikrochip zum Megaevent – Potenzen
• Wie viel mehr, wie viel weniger? – Wachstumsvorgänge
• Lügen mit Statistik – Analysieren grafischer Darstellungen
• Pythagoras und noch viel mehr – Formeln in Figuren und Körpern
• Winkel , das Messen hat ein Ende – Trigonometrie, Berechnungen an rechtwinkligen Dreiecken
• Das sieht euch ähnlich – Ähnliche Figuren, Strahlensätze

Funktionsuntersuchungen

Der Graph gibt die Geschwindigkeit eines Autos während einer Fahrt an. Mithilfe des Graphen lässt sich bestimmen, wann das Auto beschleunigt, abbremst oder stehen bleibt.

Wahrscheinlichkeitsrechnung

• Wahrscheinlichkeiten helfen uns dabei, Prognosen nicht nur „aus dem Bauch heraus“ zu treffen.
• Bedingte Wahrscheinlichkeiten erklären, warum Produkte meist mit prominenten und attraktiven Models beworben werden.

Exponentialfunktionen

In einem Gartenbuch wächst eine Lilie, die jeden Tag auf die doppelte Größe wächst. Innerhalb von dreißig Tagen kann die Lilie den ganzen Teich bedecken und alles andere Leben in dem Wasser ersticken. Aber ehe sie nicht mindestens die Hälfte der Wasseroberfläche einnimmt, erscheint ihr Wachstum nicht beängstigend; es gibt ja noch genügend Platz, und niemand denkt daran, sie zurückzuschneiden, auch nicht am 29. Tag; noch ist ja die Hälfte des Teiches frei.

Im Mathematik Grundkurs beschäftigen wir uns mit drei großen Themenbereichen der Mathematik: der Analysis, der analytischen Geometrie und der Stochastik.

In der Analysis werden systematisch die gängigen Funktionenklassen untersucht und in vielfältiger Hinsicht zur Modellbildung, beziehungsweise zum Beschreiben von Vorgängen in Wirtschaft, Natur und Gesellschaft eingesetzt. Dies entspricht insbesondere den Anforderungen, die im Rahmen des Zentralabiturs für alle Schüler des Grundkurses gelten. Konkret werden wir uns mit ganzrationalen Funktionen beschäftigen und für diese zum Beispiel Extrempunkte und Wendepunkte bestimmen. Dazu kommen dann Exponentialfunktionen, die im Zusammenspiel mit ganzrationalen Funktionen eine sehr große Bandbreite von zum Beispiel Wachstumsvorgängen beschreiben können. Anders als in Leistungskurs werden dann keine Logarithmusfunktionen und gebrochen-rationale Funktionen ins Auge gefasst. Weitere Begriffe, denen die Schüler im Bereich der Analysis begegnen, sind unter anderem: Ableitung, Aufleitung, Integral, notwendiges Kriterium, hinreichendes Kriterium, Maximum, Minimum, Extremum, Optimum, uvm.

Im Bereich der analytischen Geometrie geht es darum, ein Verständnis des uns umgebenden Raums so zu entwickeln, dass zum Beispiel die Flugbahn von Objekten in diesem Raum mathematisch höchst präzise beschrieben werden kann. Im Rahmen des Unterrichts werden verschiedene Verfahren zum Beispiel zur Abstandsbestimmung, zur Flächenberechnung, zur Volumenberechnung oder zur Winkelbestimmung erarbeitet. Darüber hinaus werden auch grundsätzliche geometrische Fragestellungen bearbeitet.

In der Stochastik wird an bekannte Modellvorstellungen angeknüpft, wie dem Erstellen eines Baumdiagramms. An Beispielen aus Spielsituationen werden die unterschiedlichen Vorstellungen von Wahrscheinlichkeiten zusammengeführt und bewertet. Damit sollen unter anderem auch Vorhersage-Wahrscheinlichkeiten für weitere Handlungsoptionen oder Spielzüge plausibel gemacht werden können. In vielen Situationen wird dabei der „gesunde Menschenverstand“ kritisch reflektiert. Anders als im Leistungskurs wird im Grundkurs nur die Binomialverteilung vertieft erarbeitet, so dass stetige Zufallsgrößen keine Rolle spielen. Gleiches gilt auch für das Testen von Hypothesen.

In großem Umfang des Oberstufenmathematikunterrichts wird dabei unser Taschenrechner, der TI 84+ CET, zum Einsatz kommen. Dieser ermöglicht es den Schülern langwierige Berechnungen, die in der Regel für ein vertieftes Verständnis nicht weiter benötigt werden, präzise durchführen zu lassen. Damit rückt der Fokus vom reinen schematischen Manipulieren von Formeln hin zu einem Erfassen und Darstellen von mathematischen Zusammenhängen.

Auch im Grundkurs wird großer Wert darauf gelegt, dass die den eigenen Berechnungen zu Grunde liegenden Ideen und Gedankenskizzen in angemessener Weise sprachlich präzisiert und dokumentiert werden. Weiterhin müssen diese angemessen mit Hilfe der Fachsprache schriftlich notiert werden können. Dies entspricht auch den seit wenigen Jahren veränderten Anforderungen des Zentralabiturs in Nordrhein-Westfalen.

Ziel eines Grundkurses ist es, ein grundlegendes Verständnis der drei mathematischen Themenbereiche zu vermitteln und trotz anderer Schwerpunkte das Interesse an mathematischen Zusammenhängen nicht zu verlieren.

Im Mathematik Leistungskurs beschäftigen wir uns mit drei großen Themenbereichen der Mathematik: der Analysis, der analytischen Geometrie und der Stochastik.

In der Analysis werden systematisch die gängigen Funktionenklassen untersucht und in vielfältiger Hinsicht zur Modellbildung, beziehungsweise zum Beschreiben von Vorgängen in Wirtschaft, Natur und Gesellschaft eingesetzt. Dies entspricht insbesondere den Anforderungen, die im Rahmen des Zentralabiturs für alle Schüler des Leistungskurses gelten. Konkret werden wir uns mit ganzrationalen Funktionen beschäftigen und für diese zum Beispiel Extrempunkte und Wendepunkte bestimmen. Dabei werden wir auch ganze Scharen von Funktonen betrachten, bei denen ein oder mehrere Parameter eine Rolle spielen. Dazu kommen dann Exponentialfunktionen, die im Zusammenspiel mit ganzrationalen Funktionen eine sehr große Bandbreite von zum Beispiel Wachstumsvorgängen beschreiben können. Vertiefend werden dann auch Logarithmusfunktionen und gebrochen rationale Funktionen ins Auge gefasst. Hier wird dann unter anderem auf asymptotisches Verhalten eingegangen. Weitere Begriffe, denen die Schüler im Bereich der Analysis begegnen, sind unter anderem: Ableitung, Aufleitung, Integral, uneigentliches Integral, notwendiges Kriterium, hinreichendes Kriterium, Maximum, Minimum, Extremum, Optimum, uvm.

Im Bereich der analytischen Geometrie geht es darum, ein Verständnis des uns umgebenden Raums so zu entwickeln, dass zum Beispiel die Flugbahn von Objekten in diesem Raum mathematisch höchst präzise beschrieben werden kann. Im Rahmen des Unterrichts werden verschiedene Verfahren zum Beispiel zur Abstandsbestimmung, zur Flächenberechnung, zur Volumenberechnung oder zur Winkelbestimmung erarbeitet. Im Weiteren erfolgt eine Beschäftigung mit Abständen so, dass zum Beispiel beurteilt werden kann, wie nah sich zwei Flugobjekte kommen können. Darüber hinaus werden auch grundsätzliche geometrische Fragestellungen bearbeitet.

In der Stochastik wird an bekannte Modellvorstellungen angeknüpft, wie dem Erstellen eines Baumdiagramms. An Beispielen aus Spielsituationen werden die unterschiedlichen Vorstellungen von Wahrscheinlichkeiten zusammengeführt und bewertet. Damit sollen unter anderem auch Vorhersage-Wahrscheinlichkeiten für weitere Handlungsoptionen oder Spielzüge plausibel gemacht werden können. In vielen Situationen wird dabei der „gesunde Menschenverstand“ kritisch reflektiert. Im Verlauf der Unterrichtsreihe werden zunehmend theoretische Modelle auch zur Simulation betrachtet. Insbesondere geht es darum, diverse Wahrscheinlichkeitsverteilungen zur möglichst präzisen Modellierung auszuwählen und einzusetzen: mithilfe der Binomialverteilung lässt sich zum Beispiel eine durchschnittliche Wartedauer berechnen; es lässt sich mithilfe der Normalverteilung die durchschnittliche Ausschussquote bei einem Produktionsprozess voraus sagen und man gelangt im Unterricht zu einem Verständnis der Voraussagegenauigkeit von Stichproben.

In großem Umfang des Oberstufenmathematikunterrichts wird dabei unser Taschenrechner, der TI 84+ CET, zum Einsatz kommen. Dieser ermöglicht es den Schülern langwierige Berechnungen, die in der Regel für ein vertieftes Verständnis nicht weiter benötigt werden, präzise durchführen zu lassen. Damit rückt der Fokus vom reinen schematischen Manipulieren von Formeln hin zu einem Erfassen und Darstellen von mathematischen Zusammenhängen.

So legen wir im Leistungskurs sehr großen Wert darauf, dass die den eigenen Berechnungen zu Grunde liegenden Ideen und Gedankenskizzen in angemessener Weise sprachlich präzisiert und dokumentiert werden. Weiterhin müssen diese präzise mit Hilfe der Fachsprache schriftlich notiert werden können. Dies entspricht auch den seit wenigen Jahren veränderten Anforderungen des Zentralabiturs in Nordrhein-Westfalen.

Ziel eines Leistungskurses bleibt wie seit jeher die Studierfähigkeit. Damit meinen wir: Am Ende des Durchgangs eines Leistungskurses Mathematik sollen unsere Schüler mit einem guten Werkzeugkoffer ausgestattet sein, um ein mathematisches oder naturwissenschaftliches Studium erfolgreich abschließen zu können.

Jede Lehrerin und jeder Lehrer erläutert euch zu Beginn des Schuljahres, nach welchen Grundsätzen die Leistungsbewertung erfolgt, was alles unter den Bereich Sonstige Leistungen im Unterricht / Sonstige Mitarbeit fällt und welches Gewicht die einzelnen Beurteilungsbereiche bei der Bildung der Gesamtnote haben werden.

Sonstige Mitarbeit

Sonstige Leistungen umfasst im wesentlichen drei Aspekte:

1. die Qualität und Quantität eurer Beiträge zum Unterrichtsgespräch

2. eure Arbeitshaltung und Arbeitsweise in Übungsphasen

3. alle anderen Präsentations- und Lernfomen (Referate, Projekte, Präsentationen usw.)

1. mündliche Mitarbeit: In Lernsituationen gehören Fehler dazu!

Wer kennt das nicht: Aus Unsicherheit, das Ergbnis einer Aufgabe könnte falsch sein, meldest du dich lieber nicht. Oder noch schlimmer: Irgendwie hast den roten Faden verloren, weil du an einem Rechenschritt hängen geblieben bist, den du nicht verstehst. Oder: …

Es gibt häufiger Situationen im Mathematikunterricht, in denen Schüler_innen schweigen, weil sie Angst haben, etwas Falsches zu sagen. Wir, eure MathematiklehrerInnen, raten euch aber lieber dazu, mutig zu sein und auch mal das Risiko einzugehen, etwas Falsches zu sagen oder eure Fragen zu stellen! Denn die Bewertung der sonstigen Mitarbeit ist gar nicht ausschließlich auf fachlich richtige Beiträge ausgerichtet. Vielmehr bezieht sie Fragehaltungen, begründete Vermutungen, sichtbare Bemühungen um Verständnis und Ansätze mit in die Bewertung ein.

Sehr häufig ist es sogar so, dass im Unterricht dadurch gelernt werden kann, dass gemeinsam überlegt wird, warum ein Ergebnis oder ein Ansatz falsch ist! Fehler gehören nämlich zum Lernprozess dazu, sie im Unterricht zu machen, heißt nicht automatisch, schlecht bewertet zu werden!

In Klausuren ist dies freilich anders – dies sind auch keine Lernsituationen, sondern Leistungssituationen. Zwar bewerten wir hier auch eure Ansätze sowie die Nachvollziehbarkeit und Vollständigkeit eurer Lösungsdarstellungen, aber die fachliche Richtigkeit zählt hier mehr.

2. Übungsaufgaben:

Regelmäßigkeit, Vollständigkeit und Qualität der Übungsaufgaben werden von uns angemessen berücksichtigt. Dabei ist vor allem euer Bemühen entscheidend, Aufgaben auf eurem Niveau zu bearbeiten. Wir erwarten von euch also in den Übungsphasen nicht, dass ihr die schnellste seid, die alles richtig hat. Vielmehr erwarten wir, dass ihr konzentriert, gewissenhaft und ordentlich arbeitet. In der Mathematik ist wie im Sport: Übung macht den Meister.

3. alle anderen Präsentations- und Lernfomen:

Die weiteren gängigen Formen der sonstigen Mitarbeit und ihre kriterienspezifische Gewichtung werden im Leistungsbewertungskonzept der Schule ausführlich erläutert. (Es gibt: Unterrichtsgespräch, Partner- und Gruppenarbeit, Hausaufgaben, Lerndokumentationen & Referate / Präsentationen/ Projekte)

Kriterien für die Überprüfung der sonstigen Leistungen

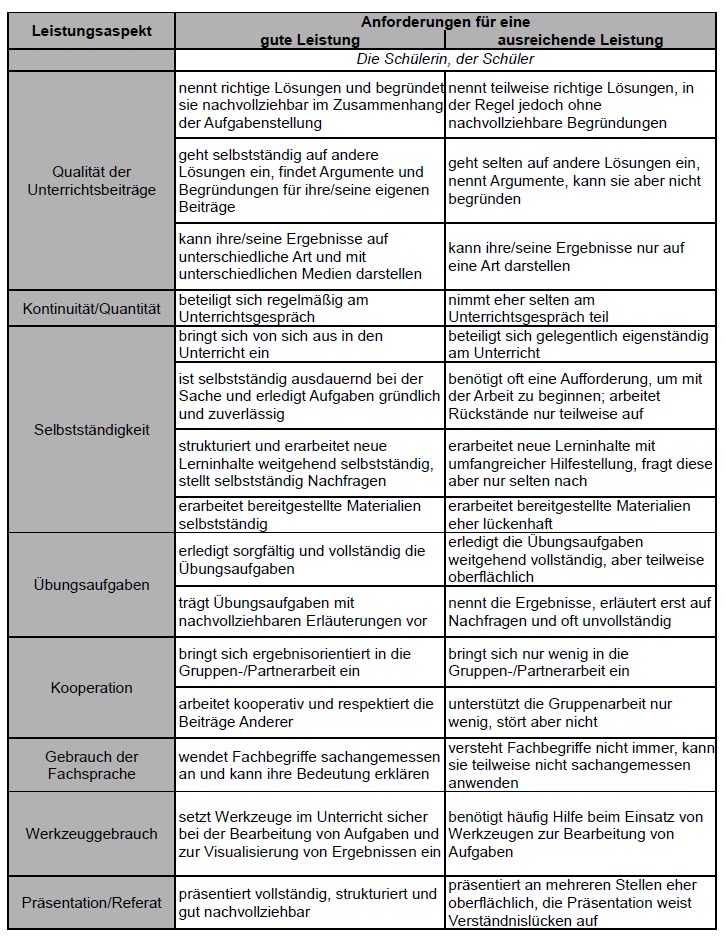
Im Folgenden werden Kriterien für die Bewertung der sonstigen Leistungen jeweils für eine gute bzw. eine ausreichende Leistung dargestellt:

Klassenarbeiten

Mathematik Klassenarbeiten bestehen zu einem großen Teil aus Rechenaufgaben. Bei diesen Aufgaben zählt aber nicht nur das Ergebnis, sondern der Ansatz und der gewählte Rechenweg gehören auch dazu! So werden bei der Korrektur von Klassenarbeiten auch Teillösungen und Lösungsansätze angemessen berücksichtigt. Stellt ein Schüler z.B. fest, dass sein Lösungsweg einen Fehler enthält, weil z.B. das Ergebnis nicht plausibel erscheint, und er verdeutlicht dies durch einen Kommentar, so wird dies in der Bewertung positiv berücksichtigt.

Darüber hinaus gehören zu den schriftlichen Arbeiten aber auch Aufgaben, die Begründungen, Darstellungen von Zusammenhängen, Interpretationen und kritische Reflexionen ermöglichen – denn auch diese Tätigkeiten gehören zur Mathematik dazu.

Die Aufgabenstellungen sollen allen drei Anforderungsniveaus entsprechen: je ca. 20% dem einfachen und komplexen Niveau, ca. 60% dem mittleren Anforderungsbereich.

Zusätzlich sollen Aufgabentypen einbezogen werden, wie sie in Lernstandserhebungen auftreten.

In Klasse 8 und 9 ist den Fachlehrer_innen freigestellt, ob sie einzelne Arbeiten mit einem GTR freien Teil und einem Teil, in dem gerade die sinnvolle Nutzung des GTR überprüft wird, konzipieren.

Kriterien für die Bewertung von Klassenarbeiten

Die Bewertung der schriftlichen Leistungen in Klassenarbeiten erfolgt über ein Raster mit Hilfspunkten, die im Erwartungshorizont den einzelnen Kriterien zugeordnet sind.

Prozentuale Notenraster für die Unter- & Mittelstufe
Wenn ihr schon Prozentrechnung hattet, müsstet ihr selbst ausrechnen können, wie viele Punkte ihr braucht, um eine bestimmte Note zu bekommen. Denn die Mathe-Lehrer*innen haben beschlossen, dass die Zuordnung der Schulnoten zu den prozentualen Anteilen der Klassenarbeitspunkte jeweils für die Unter- und die Mittelstufe vereinheitlicht wird:

In der Unterstufe (Klassen 5 & 6) muss die Note ausreichend minus bei Erreichen von 50% der Hilfspunkte erteilt werden. Die weiteren Notenabstufungen müssen (annähernd) gleichverteilt verteilt werden.

In der Mittelstufe (Klasse 7, 8 & 9) muss die Note ausreichend minus bei Erreichen von 45% der Hilfspunkte erteilt werden. Die weiteren Notenabstufungen müssen (annähernd) gleichverteilt verteilt werden.

Bei der Korrektur von Klausuren ist ferner darauf zu achten, dass von den im jeweiligen Erwartungshorizont genannten Zuordnungsschemata im Einzelfall begründet abgewichen werden kann, wenn sich z.B. besonders originelle Teillösungen nicht durch Hilfspunkte gemäß den Kriterien des Erwartungshorizontes abbilden lassen oder eine Abwertung wegen einer besonders schwacher Darstellung angemessen erscheint.

Ergebnisse bei Lernstandserhebungen:

Die Ergebnisse von Lernstandserhebungen werden mit euch detailliert besprochen – sie haben jedoch keinen Einfluss auf eure Mathe-Noten!

Sonstige Mitarbeit

In die Bewertung der sonstigen Mitarbeit fließen folgende Aspekte ein, die den Schülerinnen und Schülern bekanntgegeben werden müssen:

• Beteiligung am Unterrichtsgespräch (Quantität und Kontinuität)

• Qualität der Beiträge (inhaltlich und methodisch)

• Eingehen auf Beiträge und Argumentationen von Mitschülerinnen und
  -schülern, Unterstützung von Mitlernenden

• Umgang mit neuen Problemen, Beteiligung bei der Suche nach neuen Lösungswegen

• Selbstständigkeit im Umgang mit der Arbeit

• Umgang mit Arbeitsaufträgen (Hausaufgaben, Unterrichtsaufgaben…)

• Anstrengungsbereitschaft und Konzentration auf die Arbeit

• Beteiligung während kooperativer Arbeitsphasen

• Darstellungsleistung bei Referaten oder Plakaten und beim Vortrag von Lösungswegen

• Ergebnisse schriftlicher Übungen

• Erstellen von Protokollen

• Anfertigen zusätzlicher Arbeiten, z.B. eigenständige Ausarbeitungen im Rahmen binnendifferenzierender Maßnahmen

Die weiteren gängigen Formen der sonstigen Mitarbeit und ihre kriterienspezifische Gewichtung werden im Leistungsbewertungskonzept der Schule ausführlich erläutert. (Unterrichtsgespräch, Partner- und Gruppenarbeit, Hausaufgaben, Lerndokumentationen & Referate / Präsentationen/ Projekte)

Kriterien für die Überprüfung der sonstigen Leistungen

Im Folgenden werden Kriterien für die Bewertung der sonstigen Leistungen jeweils für eine gute bzw. eine ausreichende Leistung dargestellt. Dabei ist bei der Bildung der Quartals- und Abschlussnote jeweils die Gesamtentwicklung der Schülerin bzw. des Schülers zu berücksichtigen, eine arithmetische Bildung aus punktuell erteilten Einzelnoten erfolgt nicht:

Klausuren

Bei der Formulierung von Aufgaben werden die für die Abiturprüfungen geltenden Operatoren des Faches Mathematik schrittweise eingeführt, erläutert und dann im Rahmen der Aufgabenstellungen für die Klausuren benutzt.

Während aller Klausuren können in den Teilen mit GTR Formelsammelungen benutzt werden, die vom Fachlehrer zur Verfügung gestellt werden. Das Bedienen des GTR jedoch gehört wesentlich zum Unterrichtsinhalt, Hilfestellungen dazu werden in Klausuren sowie im Abtiur nicht gegeben.

Im Abitur gibt es einen alle Teilgebiete umfassenden hilfsmittelfreien Teil, der ohne GTR und ohne Formelsammlung bewältigt werden muss. Pro Jahr wird ab der EF mindestens (!) eine Klausur mit einem solchen Teil gestellt.

Weiterhin gelten folgende Bestimmungen:

• Die Bewertung der schriftlichen Leistungen in Klausuren erfolgt über ein Zuordnungsschemata mit Hilfspunkten, die im Erwartungshorizont den einzelnen (Teil-)leistungskriterien zugeordnet sind.

• Von den genannten Zuordnungsschemata kann im Einzelfall begründet abgewichen werden, wenn sich z.B. besonders originelle Teillösungen nicht durch Hilfspunkte gemäß den Kriterien des Erwartungshorizontes abbilden lassen oder eine Abwertung wegen besonders schwacher Darstellung (APO-GOSt §13 (2)) angemessen erscheint.

• In Klausuren sind sowohl in der Einführungs- als auch in der Qualifikationsphase alle Anforderungsbereiche zu berücksichtigen, wobei der Anforderungsbereich II den Schwerpunkt bildet. Außerdem sollen Aufgabenstellungen vorkommen, die prozessbezogene Kompetenzen wie argumentieren, begründen usw. fordern.

• Die Zuordnung der prozentualen Anteile der Hilfspunktsumme zu den Notenstufen sowohl in der Einführungsphase als auch in der Qualifikationsphase ist in den Grund- und Leistungskursen an das Zuordnungsschema des Zentralabiturs angeglichen. Demnach muss die Note ausreichend minus bei einem Erreichen von bis zu 40% der Notenpunkte erteilt werden. Die weiteren Notenabstufungen müssen (annähernd) äquidistant verteil werden.